Большинство открытий в науке делается на основе научных предположений, которые называются гипотезами (ὑπόθεσις). Гипотезы представляют собой совокупность взаимосвязанных умозаключений, не дающих категорического ответа, но позволяющих выдвинуть научное предположение. 

Признаки научной гипотезы:

• логическая непротиворечивость;
• принципиальная экспериментальная проверяемость;
• непротиворечие проверенным фактам;
• приложимость к широкому кругу явлений. 

Гипотезы, в отличие от аксиом, требуют доказательства, то есть логической операции, в процессе которой обосновывается истинность какого-либо суждения на основе других, уже доказанных суждений. Операция, доказывающая ложность какого-либо суждения, называется опровержением. 

Схема взята с сайта https://shoes-web.ru/ponyatie/i/struktura/dokazatelstva/https://shoes-web.ru/ponyatie/i/struktura/dokazatelstva/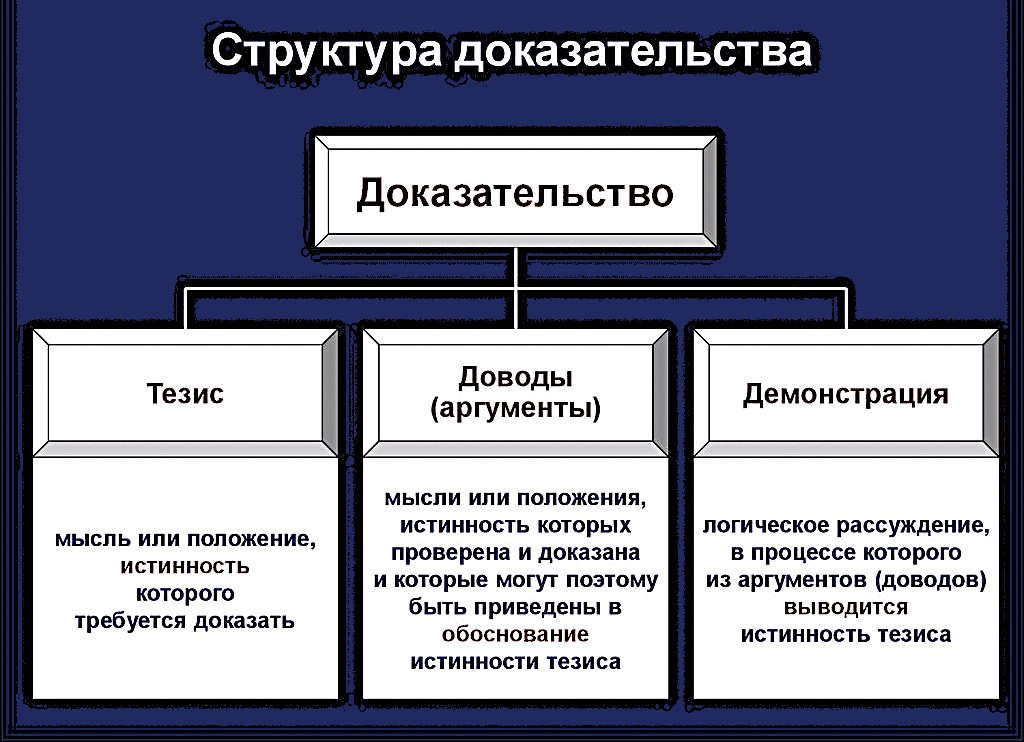 

 Правила доказательства:

1. Тезис должен быть определённым, ясно и чётко сформулированным.
2. Тезис должен быьт неизменным, тождественным самому себе.
3. Аргументы должны представлять собой истинные и доказанные суждения.
4. Аргументы должны обосновываться независимо от тезиса.
5. Аргументы не должны противоречить друг другу. 
6. Аргументы должны быть достаточными для данного тезиса.
7. Обоснование доказательства/опровержения должно строиться по правилам соответствующего вида умозаключения.

Нарушение п.1 - выдвижение неопределённого тезиса. 

Нарушение п.2 - потеря тезиса или его полная подмена путём доказательства другого тезиса, логической диверсии или апелляции к личности оппонента. 

Нарушение п.3 - принятие за истину ложного аргумента (это является основным логическим заблуждением) или предвосхищение основания. 

Нарушение п.4 - тождество аргумента и тезиса и, как следствие, "круг" в доказательстве. 

Нарушение п.6 - поспешное или чрезмерное доказательство. 

Нарушение п.7 - мнимое следование, расширение области обсуждения, аргумент к силе, к авторитету или к невежеству.  

Распространённых ошибок при демонстрации доказательства выделяют три.

1) Переход от условного к безусловному: если аргумент истинен при определённых условиях, то это не значит, что он истинен всегда. Например, при инфекционных и вирусных заболеваниях антибиотики полезны, но это не значит, что они полезны всегда. 

2) Переход от собирательного смысла к разделительному: то, что верно для множества, не всегда верно для каждого элемента этого множества. Например, положительная характеристика школьного класса недостаточна для положительной характеристики отдельного ученика этого класса. 

3) Переход от разделительного смысла к собирательному: аргумент, истинный для одного или нескольких элементов множества, не является истинным для всего множества.